

Next: 変形効果と増光効果
Up: 重力レンズ効果とは
Previous: レンズ方程式
式(1)は与えられた真の光源の位置
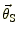 に
対して,像の位置
に
対して,像の位置
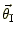 を与える非線形2元連立方程式
となっている。しかし,レンズ天体の質量分布が球対称(質量分布のレンズ天体
jの中心からの距離だけの関数)であるときは,
を与える非線形2元連立方程式
となっている。しかし,レンズ天体の質量分布が球対称(質量分布のレンズ天体
jの中心からの距離だけの関数)であるときは,
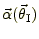 は
は
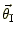 と平行
になるので,式(1)において,
と平行
になるので,式(1)において,
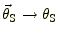 ,
,
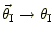 ,
,
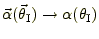 と置き換えることができる。これより,レンズ方程式を図3&4のようにグラ
フを使って解くことができる。
と置き換えることができる。これより,レンズ方程式を図3&4のようにグラ
フを使って解くことができる。
図 3:
質点レンズ
![\includegraphics[width=0.7\textwidth]{fig3.eps}](img39.png) |
図 4:
質点でない球対称レンズ
![\includegraphics[width=0.7\textwidth]{fig4.eps}](img40.png) |
図3&4では横軸を
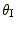 , 縦軸を
, 縦軸を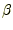 として,直線
として,直線
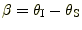 と曲線
と曲線
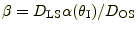 を描いたもの
である。横軸と縦軸の交点にレンズ天体があり,横軸と
を描いたもの
である。横軸と縦軸の交点にレンズ天体があり,横軸と
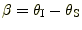 との交点に光源
との交点に光源
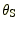 がある。そして,直線と曲線の交点の
がある。そして,直線と曲線の交点の
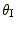 の値がレンズ方程式の解,すなわち観測される像の位置である。図3では,
レンズ天体を,質量を持つ点状の天体(質点レンズ)と近似した場合である。直線と
曲線は2点で交差していることから,このレンズ天体では1つの光源に対して2つ
の像が観測される。また,この図から光源の位置が異なれば像の位置も異なるこ
とがわかる。図4では,質点レンズでない球対称のレンズ天体を採用した場合で
ある。このレンズでは,光源が
の値がレンズ方程式の解,すなわち観測される像の位置である。図3では,
レンズ天体を,質量を持つ点状の天体(質点レンズ)と近似した場合である。直線と
曲線は2点で交差していることから,このレンズ天体では1つの光源に対して2つ
の像が観測される。また,この図から光源の位置が異なれば像の位置も異なるこ
とがわかる。図4では,質点レンズでない球対称のレンズ天体を採用した場合で
ある。このレンズでは,光源が
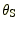 にあるときは像の数は3つ,
にあるときは像の数は3つ,
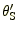 にあるときは像の数は1つであることがわかる。
にあるときは像の数は1つであることがわかる。
一般に式(1)の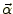 はレンズ天体の質量分布に大きく依存している。
従って,観測された像の個数や位置関係等からレンズ天体にある程度制限を与え
ることができる。
はレンズ天体の質量分布に大きく依存している。
従って,観測された像の個数や位置関係等からレンズ天体にある程度制限を与え
ることができる。
yoshidah
平成17年7月21日
![\includegraphics[width=0.7\textwidth]{fig3.eps}](img39.png)
![]() はレンズ天体の質量分布に大きく依存している。
従って,観測された像の個数や位置関係等からレンズ天体にある程度制限を与え
ることができる。
はレンズ天体の質量分布に大きく依存している。
従って,観測された像の個数や位置関係等からレンズ天体にある程度制限を与え
ることができる。