


: この文書について...
: データ解析
: 波長の測定
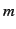 次の回折角
次の回折角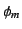 [rad]の測定にともなって測定誤差
[rad]の測定にともなって測定誤差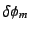 が生
じる。更に、
が生
じる。更に、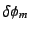 は
は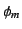 を用いて計算される波長
を用いて計算される波長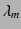 にも
にも
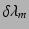 の形で現れる(誤差の伝播)。ここでは、
の形で現れる(誤差の伝播)。ここでは、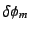 と
と
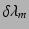 の関係を調べる。
の関係を調べる。
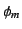 より得られる波長を
より得られる波長を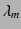 (測定値)、
(測定値)、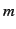 次の回折角の真値を
次の回折角の真値を
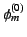 、測定している光の波長の真値を
、測定している光の波長の真値を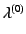 (真値は次
数によらず一定である)とする。また、格子定数についても
(真値は次
数によらず一定である)とする。また、格子定数についても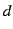 を測定値、
を測定値、
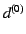 を真値、
を真値、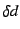 を誤差とする。このとき、
を誤差とする。このとき、
となる。ここで
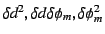 は無視し
た。また、
は無視し
た。また、
![$\phi^{(0)}_m{\rm [rad]}<1,\delta\phi_m\ll1$](img47.png) なので、
なので、
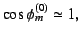
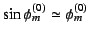 と近似で
きることを用いた。以上より、
と近似で
きることを用いた。以上より、
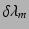 は
は
となることがわかる。
ここで、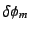 は何が原因で生じるのだろうか?まず、望遠鏡内の
は何が原因で生じるのだろうか?まず、望遠鏡内の
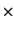 字を測定するスペクトルに合わせる際に生じる誤差
字を測定するスペクトルに合わせる際に生じる誤差
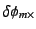 と、A・Bの目盛りを読む際に生じる誤差
と、A・Bの目盛りを読む際に生じる誤差
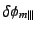 とが考えられる。
とが考えられる。
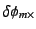 はスペクトルの
見やすさに大きく依存するので、
はスペクトルの
見やすさに大きく依存するので、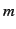 が大きくなると
が大きくなると
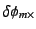 も
大きくなることが期待される。一方、
も
大きくなることが期待される。一方、
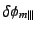 は次数が変わっても
変わらない。
は次数が変わっても
変わらない。
より、もし測定において
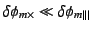 であれ
ば、
であれ
ば、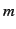 が大きいほど
が大きいほど
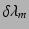 は小さくなり、一方、
は小さくなり、一方、
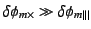 であれば、
であれば、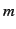 が大きいほど
が大きいほど
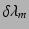 は大きくなることがわかる。
は大きくなることがわかる。
- 課題1
- 各色で
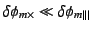 で
あったのか、
で
あったのか、
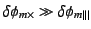 であったのかを調
べ、口述報告のときに結果と一緒に報告せよ。
であったのかを調
べ、口述報告のときに結果と一緒に報告せよ。
- 課題2
- 回折格子の分解能とはなにかを考えよ(レポートにて)。
yoshidah
平成15年2月5日
![]() より得られる波長を
より得られる波長を![]() (測定値)、
(測定値)、![]() 次の回折角の真値を
次の回折角の真値を
![]() 、測定している光の波長の真値を
、測定している光の波長の真値を![]() (真値は次
数によらず一定である)とする。また、格子定数についても
(真値は次
数によらず一定である)とする。また、格子定数についても![]() を測定値、
を測定値、
![]() を真値、
を真値、![]() を誤差とする。このとき、
を誤差とする。このとき、
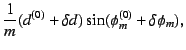
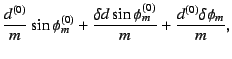
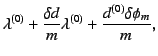
![]() は何が原因で生じるのだろうか?まず、望遠鏡内の
は何が原因で生じるのだろうか?まず、望遠鏡内の
![]() 字を測定するスペクトルに合わせる際に生じる誤差
字を測定するスペクトルに合わせる際に生じる誤差
![]() と、A・Bの目盛りを読む際に生じる誤差
と、A・Bの目盛りを読む際に生じる誤差
![]() とが考えられる。
とが考えられる。
![]() はスペクトルの
見やすさに大きく依存するので、
はスペクトルの
見やすさに大きく依存するので、![]() が大きくなると
が大きくなると
![]() も
大きくなることが期待される。一方、
も
大きくなることが期待される。一方、
![]() は次数が変わっても
変わらない。
は次数が変わっても
変わらない。