

Next: 多重効果
Up: 重力レンズ効果とは
Previous: 重力レンズ効果とは
前節で述べたように,一般相対性理論によると光は時空に沿った最短の光路を伝
播する。光路は滑らかな曲線となるが,実際にこのような曲線を扱うのは非
常に難しい。幸いレンズ天体による重力が比較的弱い場合(ブラックホールのよ
うな天体でない限り)では,この曲線は折れ線で近似できる。この近
似から得られる方程式が,重力レンズ効果での基本方程式である「レンズ方
程式」である。
図 1:
観測者,光源,レンズ天体の位置関係
![\includegraphics[width=0.9\textwidth]{fig1.eps}](img21.png) |
図 2:
光源面への射影図
![\includegraphics[width=0.5\textwidth]{fig2.eps}](img22.png) |
図1のように観測者と光源の間にレンズ天体があるとする。観測者-レンズ天体
間,観測者-光源間,レンズ天体-光源間の距離をそれぞれ
 とする。
また,レンズ天体を含み視線方向に対して垂直な平面をレンズ面,光源を含み視
線方向に対して垂直な平面を光源面と名付ける。本来重力レンズ効果を受けなけ
れば,光源はレンズ天体に対して
とする。
また,レンズ天体を含み視線方向に対して垂直な平面をレンズ面,光源を含み視
線方向に対して垂直な平面を光源面と名付ける。本来重力レンズ効果を受けなけ
れば,光源はレンズ天体に対して
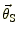 の角度(実際の観測
では知ることができないのだが)に見える筈である。しかし,レンズ天体の重力
によって光路がレンズ面で角度
の角度(実際の観測
では知ることができないのだが)に見える筈である。しかし,レンズ天体の重力
によって光路がレンズ面で角度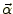 だけ曲がるので,レ
ンズ天体に対して
だけ曲がるので,レ
ンズ天体に対して
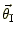 の角度のところに光源の像が観測
される。この様子を観測者から光源面へ射影したのが図2である。ここで,
の角度のところに光源の像が観測
される。この様子を観測者から光源面へ射影したのが図2である。ここで,
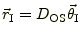 と
と
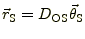 はそれぞれ光源
面に射影したレンズ天体に対する像と光源の位置である。
はそれぞれ光源
面に射影したレンズ天体に対する像と光源の位置である。
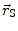 と
と
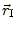 の差がレンズ効果によって光路が曲げられた結果で
の差がレンズ効果によって光路が曲げられた結果で
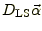 である。すなわち,
である。すなわち,
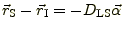 の関係が得られる。一般に,光の曲がり角
の関係が得られる。一般に,光の曲がり角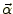 は光がレンズ面のど
こを通るのかによってきまる。従って,
は光がレンズ面のど
こを通るのかによってきまる。従って,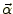 は
は
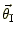 の関数で与えられる。先の式の
の関数で与えられる。先の式の
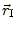 を右辺に移項して,両辺を
を右辺に移項して,両辺を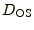 で割ったもの
が,所謂「レンズ方程式」である:
で割ったもの
が,所謂「レンズ方程式」である:
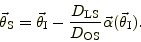 |
(1) |
yoshidah
平成17年7月21日
![\includegraphics[width=0.9\textwidth]{fig1.eps}](img21.png)